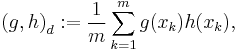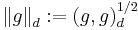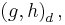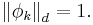Discrete Chebyshev polynomials

Not to be confused with Chebyshev polynomials.

In mathematics, discrete Chebyshev polynomials, or Gram polynomials, are a type of discrete orthogonal polynomials used in approximation theory, introduced by Pafnuty Chebyshev (1864) and rediscovered by Gram (1883).

Definition

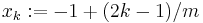They are defined as follows: Let f be a smooth function defined on the closed interval \left[-1,1\right] whose values are known explicitly only at points \textstyle x_k:=-1%2B(2k-1)/m , where k and m are integers and 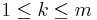1\leq k\leq m . The task is to approximate f as a polynomial of degree n < m. Now consider a positive semi-definite bilinear form

\left(g,h\right)_d:=\frac{1}{m}\sum_{k=1}^{m}{g(x_k)h(x_k)},

where g and h are continuous on \textstyle\left[-1,1\right] and let

\left\|g\right\|_d:=(g,g)^{1/2}_{d}

be a discrete semi-norm. Now let 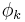\phi_k be a family of polynomials orthogonal to

\left(g,h\right)_d,

which have a positive leading coefficient and which are normalized in such a way that

\left\|\phi_k\right\|_d=1.

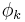The \phi_k are called discrete Chebyshev (or Gram) polynomials.[1]

References

  1. ^ R.W. Barnard; G. Dahlquist, K. Pearce, L. Reichel, K.C. Richards (1998). "Gram Polynomials and the Kummer Function". Journal of Approximation Theory 94: 128–143. doi:10.1006/jath.1998.3181.